Le compas de proportion : le couteau suisse mathématique

Instrument à fonctions multiples, le compas de proportion est décrit pour la première fois par Galilée au début du 17^e siècle. Il était très utilisé par les géomètres, ingénieurs et artisans jusqu’au milieu du 19^e siècle. Cet instrument permet de résoudre de manière géométrique de nombreux types de calculs différents : proportions, mesures d’angles, surfaces, volumes, masse volumique de métaux différents, etc.

Son principe de fonctionnement repose sur les propriétés géométriques des triangles semblables et plus précisément sur les rapports proportionnels existant entre leurs côtés homologues. Rappelons que deux triangles de taille différente sont dits semblables si leurs angles sont identiques.

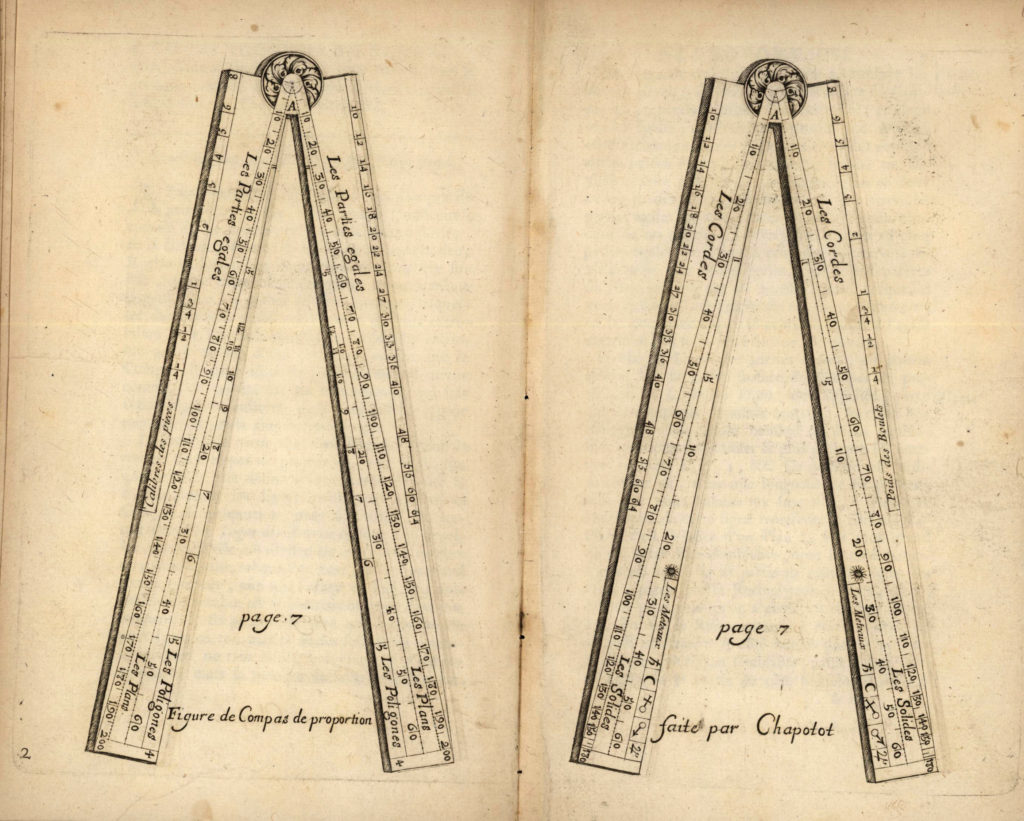
Le compas de proportion est constitué de deux règles plates de même dimension (les jambes), généralement en laiton, reliées l’une à l’autre par une charnière plate à l’une de leurs extrémités. Les deux règles peuvent ainsi s’ouvrir complètement pour former une longue règle plate. En général, le compas s’utilise à différents angles d’ouverture.

A partir du centre de la charnière sont tracées différentes lignes divergentes qui aboutissent à l’extrémité de chaque branche. Disposées de manière symétrique d’une branche à l’autre, ces lignes portent différentes échelles et graduations. Ces échelles sont tracées de telles manière que l’on puisse établir commodément des rapports et des correspondances entre les graduations.

Si le compas est entrouvert, on trouve sur une face la ligne des « Parties égales », celle des « Plans » et celle des « Polygones ». Sur l’autre face, la ligne des « Cordes », celle des « Solides » et celle des « Métaux ».

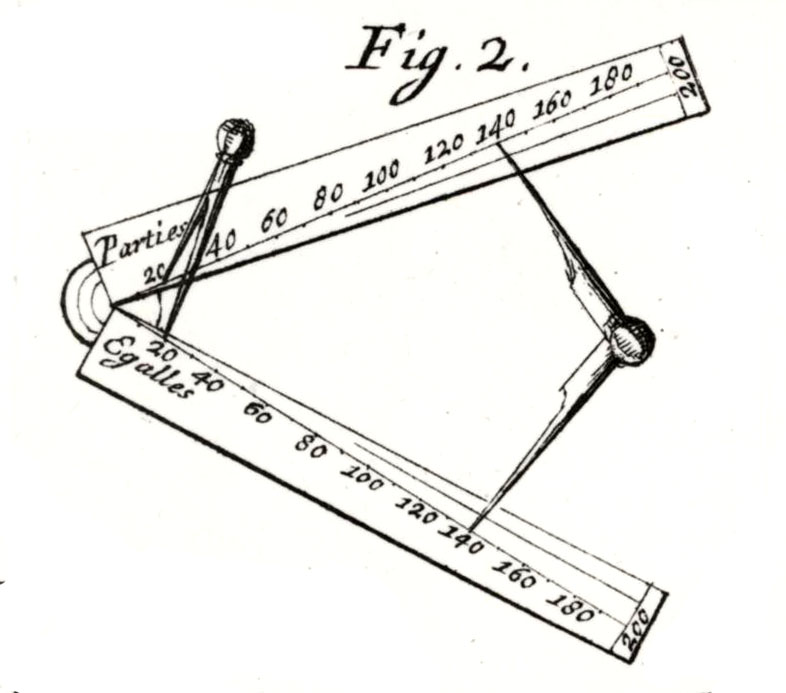
L’instrument s’utilise avec un compas à pointes sèches. Cet accessoire permet de mesurer une longueur donnée, puis de la reporter entre deux graduations identiques d’une même échelle sur chacune des branches. Tout en conservant le même écartement du compas de proportion, on se sert du compas à pointe sèche pour déterminer une grandeur recherchée en mesurant l’écartement entre deux autres graduations identiques de la même échelle.

Exemple pratique avec la ligne des Parties égales qui sert à résoudre des problèmes arithmétiques de rapport de longueurs ou des proportions.  Cette ligne est divisée en 200 intervalles égaux, numérotés de 10 en 10. Soit une droite tracée sur un plan que l’on souhaite diviser en 7 parties égales. On mesure tout d’abord sa longueur avec le compas à pointes sèches. On écarte les deux branches du compas de proportion et l’on reporte l’écartement correspondant à la longueur mesurée entre deux chiffres identiques multiples de 7 par exemple 140 et 140 situés sur les lignes des Parties égales.  En conservant la même ouverture des deux branches, on mesure alors avec les pointes sèches l’écartement entre 20 et 20 (1/7 de 140) indiqués sur les mêmes lignes. Cet écartement correspond à la septième partie de la droite.

Les compas de proportion français possèdent en général des dimensions similaires. Une branche mesure 14 mm de large et 16 à 17 cm de longueur, soit l’équivalent d’un demi-pied. La longueur totale de l’instrument vaut 1 pied de roi, l’unité de longueur en vigueur avant la Révolution française.

Le Musée d’histoire des sciences possède dans ses collections une vingtaine de compas de proportion signés par les constructeurs parisiens les plus réputés de l’époque : Nicolas Bion (1652-1733), Claude Langlois (1720-1756), Jacques Canivet (1743-1774), Claude-Siméon Passemant (1702-1769) et Michael Butterfield (1635-1724). A propos de ce dernier constructeur, ses instruments étaient tellement réputés que des artisans peu scrupuleux ont imité et reproduit sa signature sur leurs instruments. Ce qui semble être le cas de deux compas signés « Butterfield à Paris » dont la grossièreté de la gravure laisse penser qu’ils sont l’œuvre de faussaires.

Les autres lignes du compas de proportion

La ligne des Plans

Elle est divisée en 64 partie égales numérotées de 10 en 10. Elle aide à résoudre des problèmes de surface (par exemple la longueur de côtés homologues pour des surfaces doublées, triplées, quadruplées, etc.)

La ligne des Polygones

Elle comprend 9 graduations numérotées de 12 à 4. Elle donne la longueur de polygones de 4 à 12 côtés inscrits dans un cercle de rayon donné.

La ligne des Cordes

Elle est divisée en 180 parties égales de 10 en 10. C’est une échelle proportionnelle aux arcs successifs de 0 à 180° d’un demi-cercle dont le diamètre est égal à la longueur de l’échelle. Cette échelle permet des opérations sur les arcs et les angles.

La ligne des Solides

Elle est divisée de 0 à 64 de 10 en 10. Elle aide à des calculs sur des volumes, notamment à connaître des côtés homologues de volumes multiples.

La ligne des métaux

Elle porte 6 graduations correspondant aux six principaux métaux (représentés par leur symbole astronomique) utilisés à cette époque et classés selon leur densité. L’or suivi par le plomb, l’argent, le cuivre, le fer et enfin l’étain, le moins dense. Cette échelle permet de résoudre des problèmes de masse volumique et de poids de métaux.